Le présent texte a été publié pour la première fois dans le magazine Ultrafondus, en 2005.
Estimation de la difficulté d’un parcours en milieu naturel : relation de couplage dénivelé / distance
Tous les coureurs de trail se sont un jour ou l’autre trouvés devant la difficulté d’estimation des temps de parcours, que ce soit lors de compétitions ou lors d’entrainements. Cette difficulté est encore plus cruciale pour les compétitions de type « raid montagne - stratégie FFME », qui sont totalement basées sur la qualité des prévisions effectuées : pour ces compétitions, le vainqueur n’est pas forcément celui qui va le plus vite, mais plutôt celui qui sait combiner à ses qualités physiques une excellente capacité à prévoir ses forces et ses faiblesses.
Des travaux menés en 2002, et décrits en détail dans la référence [1] [Minetti AE, Moia C, Roi GS, Susta D, Ferretti G. Energy Cost of walking and running at extreme uphill and downhill slopes. J Appl Physiol 93: 1039-1046, 2002], permettent de déterminer de manière fiable la relation générique qui existe entre les paramètres dénivelé, distance et « difficulté ».
Cette étude a été menée sur un échantillon de dix coureurs aguerris. L’expérimentation consistait à les faire courir ou marcher sur tapis roulant, à différentes allures et à différentes pentes, aussi bien en pentes positives qu’en pentes négatives. Il faut noter que les pentes expérimentées allaient jusqu’à des pourcentages de 40% en côte ou en descente, pourcentages rarement rencontrés lors de parcours réels en montagne, sur chemins ou sentiers.
De manière très classique pour ce type d’expérimentation, l’énergie dépensée était estimée d’après les consommations d’oxygène. Chaque mesure était effectuée pour une expérimentation (vitesse et pente donnée) d’une durée de 4 minutes.
En reprenant les résultats numériques de l’article, on peut calculer les « équivalents kilomètres » à partir des différentes consommations d’énergie.
Il s’agit ici d’équivalents kilomètres basés uniquement sur la consommation d’énergie. Les autres paramètres de la « fatigue » (fatigue cérébrale, douleurs articulaires ou musculaires, perte d’élasticité musculaire, etc…) ne sont pas pris en compte.
Le calcul se concrétise par la courbe ci-dessous :
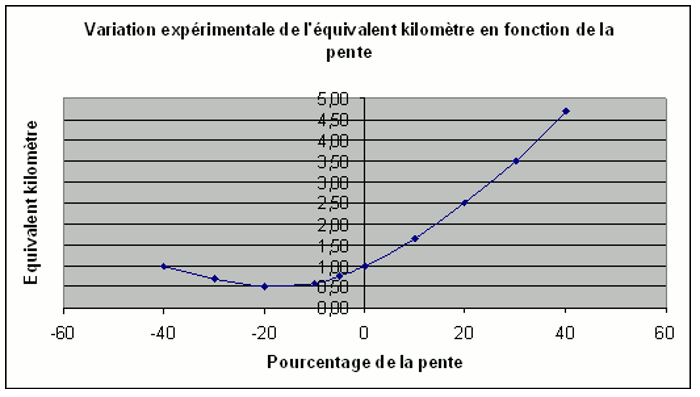
Il est alors intéressant de comparer cette courbe obtenue en laboratoire à d’autres courbes présentées dans d’autres sources.
Les comparaisons sont ici effectuées avec les courbes suivantes :
- La courbe souvent utilisée en montagne, courbe déduite de la formule « 100 mètres de dénivelé positif sont équivalents à un kilomètre sur le plat ».
- La courbe traduisant la formule donnée par Denis Riché (réf [3]).
- Une courbe donnant des vitesses de progression en randonnée en montagne, et présentée par la Fédération Suisse de Randonnée (réf [2]).
- Une courbe issue de résultats de courses effectuées uniquement en montée ou en descente (résultats extraits de [1]).
Ces courbes sont toutes présentées sur le schéma ci-dessous :
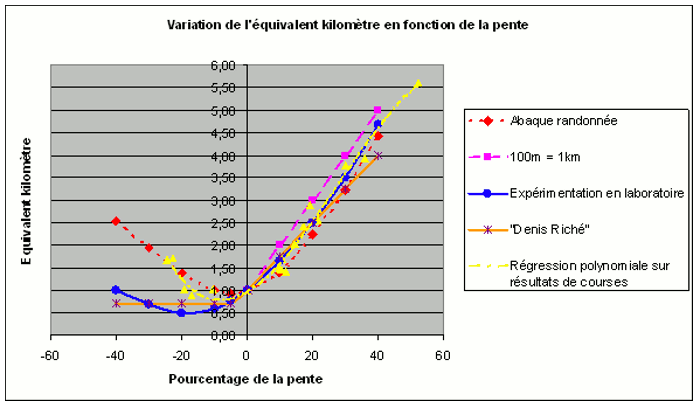
On peut noter l’étonnante proximité de ces courbes à une importante exception près : les mesures effectuées en laboratoire ne correspondent pas du tout aux différentes vitesses observées dans la pratique pour les descentes « raides ».
En accord avec les auteurs de l’article [1], on peut avancer les hypothèses suivantes pour expliquer cette différence :
- Le tapis roulant est une surface entièrement lisse et antidérapante ; cette surface ne reflète en rien les difficultés de progression à vitesse élevée, en descente raide et en terrain réel (éboulis, poussière, herbes…).
- La « casse musculaire » due aux efforts de type « excentrique » est un facteur de fatigue bien supérieur à la consommation énergétique dans ces conditions.
Calcul de la « meilleure courbe », synthèse des données terrain et des données expérimentales
Pour les raisons évoquées ci-dessus, les données d’expérimentation en laboratoire obtenues pour des pentes raides seront éliminées de la suite des calculs, car non représentatives de la réalité terrain.
Pour les descentes, on ne conservera donc que les données suivantes :
- Abaque de randonnée,
- Données de résultats de courses.
Pour les descentes, on retiendra les données issues des courbes a priori les plus précises :
- Abaque de randonnée,
- Données issues des expérimentations en laboratoire.
Sur cet ensemble de points, on effectue une régression polynomiale, opération qui nous permet d’obtenir une courbe effectuant la synthèse des données d’expérimentation et des données terrain.
Cette courbe est donnée sur le schéma suivant :
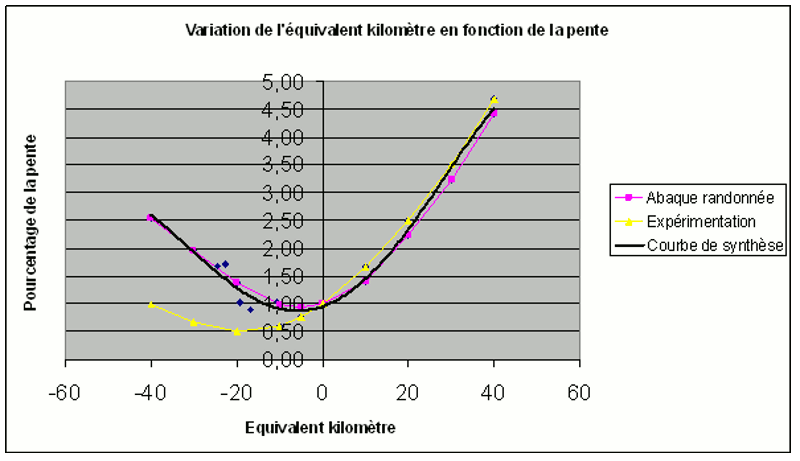
Validation des résultats obtenus sur les données de l’UTMB 2004
La courbe synthèse présentée ci-dessus a été testée sur les temps de passage réels de coureurs de l’UTMB 2004.
Le tableau ci-dessous présente la corrélation obtenue pour les temps unitaires de début de parcours de Vincent Delebarre et en utilisant un coefficient de ralentissement linéaire tout au long de cette portion.
| |
Col de Voza
|
Contamines
|
Bonhomme
|
|
Observé
|
1:23:00
|
1:06:00
|
1:54:00
|
|
Estimé
|
1:21:40
|
1:06:20
|
1:51:43
|
On observe sur cs données une très bonne corrélation entre les temps prévus et les temps observés, la différence maximum étant de 2%, pour la portion Contamines-Bonhomme.
Les temps de passage dans la suite de la course sont fortement perturbés par des temps de pause non connus. Ces données n’ont donc pas été utilisées pour la validation du modèle.
Une validation plus poussée de ce modèle de synthèse devra être effectuée sur des données plus précises et plus nombreuses, en utilisant des parcours de caractéristiques connues et des données temporelles (durées de progression, durées de pause…) complètes.
Etude de la « régularité » des parcours
Tout coureur de trail et tout randonneur a observé que la connaissance de la distance et du dénivelé n’était pas suffisante pour effectuer une estimation fiable de la durée nécessaire pour effectuer un parcours donné.
En effet, comment expliquer, par exemple, que les temps des premiers soient très proches sur l’UTMB et sur le GRR, alors que les dénivelés sont assez similaires, mais que le kilométrage est très inférieur pour le GRR ?
Les conditions météorologiques ou l’état du sol ne paraissent pas suffisants pour expliquer ce fait, vraiment très étonnant.
L’explication souvent avancée est que le GRR comporte des parties de côtes ou de descentes très raides, assez peu fréquentes sur l’UTMB. L’expérience de la course laisserait donc penser que la « régularité » des pentes serait un facteur très important sur la difficulté d’un parcours.
Ainsi, la plus forte régularité des pentes de l’UTMB rendraient son parcours « moins difficile » (s’il est permis d’employer cette expression !).
J’ai donc voulu vérifier par la simulation ce fait d’expérience.
Pour cela, j’ai utilisé un échantillon de parcours simulés, en gardant des kilométrages et des dénivelés constants, mais en faisant varier la répartition des pentes.
La formule de synthèse des équivalents kilomètres obtenue plus haut a bien évidemment été utilisée comme base pour ces simulations.
Les résultats obtenus sont les suivants :
- Les temps les plus bas sont toujours obtenus pour les parcours pour lesquel la pente est la plus régulière, aussi bien en montée qu’en descente.
- Les temps les plus élevés sont toujours obtenus pour les parcours comportant les pentes les plus raides et, de manière corrélée, les portions de plat les plus longues.
- Pour une même distance et un même dénivelé, les différences de temps peuvent aller jusqu’à 30%, en prenant les conditions extrèmes, et jusqu’à 15 % à 20 %, en prenant des situations très couramment rencontrées dans la nature.
Le graphique ci-dessous résume les différences de temps dues aux irrégularités de la pente :
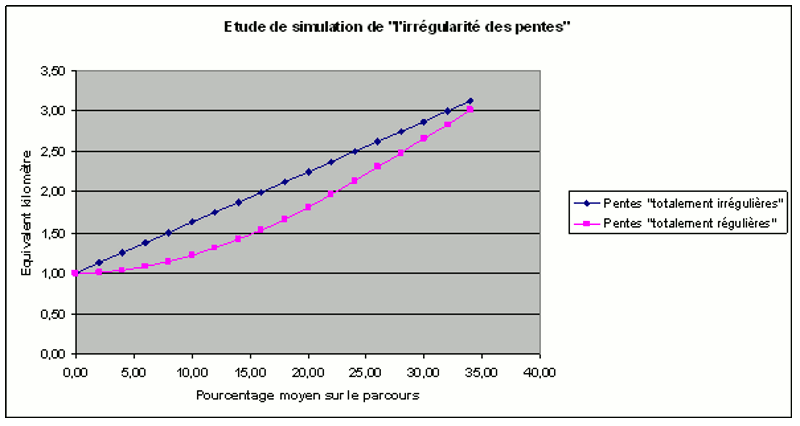
Par exemple, pour une pente moyenne de 10%, un parcours de 1 km pourra varier entre 1,22 km équivalent kilomètre au minimum (pour un parcours où toutes les pentes sont égales en valeur absolue), et 1,62 km équivalent au maximum (pour un parcours où toutes les pentes sont de 40% en valeur aboslue et où les portions restantes sont totalement plates), soit une différence de 33 %.
Validation des résultats obtenus
Pour terminer, j’ai appliqué les résultats sur la régularité des pentes, à différents trails ou courses sur route « étalon ».
Les calculs ont été effectués à partir des seules données globales sur les distances et les dénivelés positifs et négatifs. J’ai estimé la « régularité » des pentes d’après mes expériences personnelles sur ces différentes courses et sur les avis que j’ai pu entendre ou lire par ailleurs.
La validation des résultats a été effectuée par analyse de la corrélation entre les kilomètres équivalents calculés et les « temps moyens » réalisés par les premiers des courses.
Les résultats obtenus sont résumés sur le graphique et sur le tableau ci-dessous :
|
|
Distance
|
Dénivelé +
|
Dénivelé -
|
Irrégularité
|
Min
|
Max
|
Kilomètre équivalent
|
Temps
|
Moyenne kilomètrique
|
|
Marathon
|
41,20
|
0
|
0
|
0
|
41,20
|
41,20
|
41,20
|
2:20:00
|
00:03:24
|
|
Sierre Zinal
|
31,00
|
2200
|
1000
|
0,3
|
41,42
|
53,91
|
45,17
|
2:35:00
|
00:03:26
|
|
Trail des Cerces
|
48,00
|
2500
|
2500
|
0,4
|
59,23
|
79,20
|
67,22
|
4:32:00
|
00:04:03
|
|
Dents du Midi
|
44,00
|
2890
|
2890
|
0,4
|
60,18
|
80,07
|
68,13
|
04:30:00
|
00:03:58
|
|
Templiers
|
65,00
|
2600
|
2600
|
0,4
|
74,05
|
97,45
|
83,41
|
5:55:00
|
00:04:15
|
|
100km
|
100,00
|
0
|
0
|
0
|
100,00
|
100,00
|
100,00
|
7:10:00
|
00:04:18
|
|
Cro-Magnon
|
106,40
|
4456
|
5456
|
0,5
|
123,64
|
165,80
|
144,72
|
12:27:00
|
00:05:10
|
|
Mercantour
|
102,00
|
5873
|
5873
|
0,4
|
131,04
|
175,30
|
148,74
|
12:37:00
|
00:05:05
|
|
EUT
|
111,00
|
5300
|
5300
|
0,35
|
132,90
|
177,14
|
148,39
|
12:08:00
|
00:04:54
|
|
GRR
|
130,00
|
8385
|
8385
|
0,55
|
176,15
|
234,64
|
208,32
|
20:00:00
|
00:05:46
|
|
UTMB
|
157,00
|
8600
|
8600
|
0,25
|
197,55
|
264,33
|
214,24
|
21:00:00
|
00:05:53
|
|
24h
|
235,00
|
0
|
0
|
0
|
235,00
|
235,00
|
235,00
|
24:00:00
|
00:06:08
|
On observe les points suivants :
- La courbe obtenue en utilisant des « coefficients d’irrégularité ajustés » donne les meilleurs résultats.
- La courbe obtenue en utilisant des coefficients d’irrégularité tous égaux à 0,45 donne des résultats légèrement moins bons, mais néanmoins nettement meilleurs que ceux obtenus en utilisant la formule : « équivalent-kilomètre = distance en km + dénivelé en centaines de mètres ».
Le « réglage » des coefficients d’irrégularité se heurte à sa difficulté d’appréciation pour un parcours encore jamais pratiqué, appréciation contenant obligatoirement une part de subjectivité. Cependant, on voit que l’utilisation du modèle avec un coefficient d’irrégularité moyen de 0,45 donne le plus souvent des résultats satisfaisants.
Il est bien évidemment toujours plus précis et plus fiable d’effectuer l’estimation de la difficulté d’après le profil détaillé exact des parcours de course, lorsque ces données sont disponibles.
Conclusion
Malgré tout le soin et la rigueur apportés aux différentes opérations, les résultats présentés ici ne doivent pas être pris comme des résultats de travaux scientifiques, mais comme des pistes de réflexion et d’expérimentation.
Les différents résultats peuvent d’ores et déjà être mis en pratique au travers de calculateurs, en restant bien entendu prudent sur l’usage qui en est fait : un trail longue distance est soumis à un ensemble très important d’aleas autres que les pentes rencontrées, et qui échappent très souvent à toute prévision.
Par ailleurs, les axes suivants n’ont pas été abordés ici, et pourront faire l’objet d’études complémentaires :
- Importance relative des différents facteurs de fatigue dans une course en terrain varié, et notamment influence de la dégradation progressive de l’équilibre, de la souplesse, de l’élasticité musculaire, etc.
- Forme générale de la courbe de ralentissement de la vitesse en fonction du temps ; question de la linéarité ou de la non linéarité.
- Influence de la gestion de course : temps de pause, temps de marche et temps de course (« méthode Cyrano »), en descente et en montée, etc.
Références :
[1] : Minetti AE, Moia C, Roi GS, Susta D, Ferretti G. Energy Cost of walking and running at extreme uphill and downhill slopes. J Appl Physiol 93: 1039-1046, 2002 / Voir ici le pdf de cet article.
[2] : Walking time estimates for trail ; https://rjd.home.cern.ch/rjd/Walk/speed.html
[3] : Riché D. Guide nutritionnel des sports d’endurance, 2ème édition. Vigot, 1998








